Scheepsstabiliteit

De Cougar Ace met een slagzij van 60° door verlies van stabiliteit tijdens ballastwateruitwisseling.

Scheepsstabiliteit is de mate waarin een schip zichzelf weer op kan richten na uit zijn evenwicht te zijn gebracht. Met de wet van Archimedes werd ruim twee eeuwen voor het begin van de jaartelling een aanvang gemaakt met de stabiliteitstheorie. Een te kleine stabiliteit kan leiden tot het kapseizen van een schip. Het is daarom wettelijk verplicht om op zeeschepen de stabiliteit uit te rekenen voor aanvang van de reis, zodat bekend is of deze veilig kan worden ondernomen.

Inleiding

Aanvangsstabiliteit

Statisch

Kleine hellingen

Dwarsscheeps

Dynamisch

Grote hellingen

Stabiliteit

Statisch Ψ < 7°

Dokstabiliteit

Langsscheeps

Dynamisch

Lekstabiliteit

Stabiliteit is afhankelijk van de scheepsvorm en van de belading. De scheepsbouwer is verantwoordelijk voor het eerste, de stuurman voor het laatste. Afhankelijk van het ontwerp van het schip heeft de stuurman meer of minder mogelijkheden om de belading te plannen.

Stabiliteit is op verschillende manieren onder te verdelen. Allereerst zijn er de dwarsscheepse en langsscheepse stabiliteit. Dit is de mate van richtend moment in dwarsscheepse en langsscheepse richting. Dit is weer verder onder te verdelen. Zo wordt verschil gemaakt tussen stabiliteit bij kleine en grote hellingshoeken. Gebaseerd op de aanname dat het metacentrum zich niet wezenlijk verplaatst bij kleine hoeken, maakt men in die gevallen gebruik van de aanvangsstabiliteit.

Ook is er onderscheid te maken tussen statische en dynamische stabiliteit. Bovenstaand zijn voorbeelden van statische stabiliteit, waarbij de toestand van het schip wordt beschouwd in rusttoestand of geleidelijk veranderende krachten. Bij plotselinge optredende krachten, zoals een windstoot of het overgaan van graan, spreekt men van dynamische stabiliteit. Het gevaar hierbij is dat het schip verder doorslingert bij een plotselinge windstoot dan bij een constante windkracht. De helling die bereikt wordt, rekent men uit door de arbeid te bepalen die daarvoor verricht moet worden.

Naast de hiervoor beschreven intacte stabiliteit moet ook rekening worden gehouden met de lekstabiliteit. Mocht een schip door aanvaring of gronding lek raken, dan is het niet alleen zaak dat er voldoende reservedrijfvermogen is, er moet ook voldoende stabiliteit zijn. In het ontwerp van de waterdichte indeling van een schip moet hier al rekening mee worden gehouden. Dit doet men aan de hand van probabilistische lekberekening. Als een deel van een schip lek is geraakt, kan het effect hiervan met de deterministische lekberekening worden bepaald.

Bij zeilschepen spreekt men van begin- en eindstabiliteit. Een grote aanvangsstabiliteit wordt bereikt met brede schepen, een grote eindstabiliteit door een laag zwaartepunt, bijvoorbeeld door een zware kiel.

Geschiedenis

Archimedes

Drijfvermogen

In de vierde eeuw v.Chr. gaf Aristoteles in De Caelo (Over de Hemel) aan dat het drijfvermogen van een lichaam afhankelijk was van het relatieve gewicht van een materiaal in een medium en de vorm van het lichaam.

Ruim een eeuw later, rond 220 v.Chr., stelde Archimedes de bepalingen op voor de hydrostatische stabiliteit van drijvende lichamen. In eerder werk had hij al het begrip zwaartepunt geïntroduceerd, waarbij hij oppervlaktes, volumes en gewichten terugbracht tot punten met dezelfde eigenschappen, zoals het massamiddelpunt. In het eerste boek van zijn werk Over drijvende lichamen stelde hij: 'elke vaste stof die lichter is dan een vloeistof, zinkt zover in dat het gewicht van de verplaatste vloeistof gelijk is aan het gewicht van de vaste stof'. Tegenwoordig wordt dit geschreven als:

<math>\Delta = \rho \cdot V</math>

waarbij <math>\Delta</math> de massa is, <math>\rho</math> de dichtheid van de vloeistof en V het verplaatste volume. Hoewel Archimedes het bij het rechte eind had, werden lange tijd de ideeën van Aristoteles aangehangen. Nog in 1611 moest Galileo Galilei de ideeën van Archimedes verdedigen tegenover die van Aristoteles. In 1612 legde hij dit vast in Discorso intorno alle cose che stanno in su l'acqua (Verhandelingen over drijvende lichamen).

Richtend moment

In het tweede boek behandelde Archimedes het hydrostatische evenwicht van een segment van een omwentelingsparaboloïde. Hij stelde dat de opwaartse kracht aangrijpt in het drukkingspunt, terwijl het gewicht aangrijpt in het zwaartepunt, waarbij de krachten even groot zijn, maar tegengesteld. Zodra het lichaam uit evenwicht wordt gebracht, treedt er een richtend moment op dat het lichaam terugbrengt in de ruststand. Hoewel de benadering die Archimedes koos slechts toepasbaar was op homogene parabolische vormen, legde Archimedes hiermee de basis voor latere scheepsstabiliteit. Zijn werk werd in 1269 vertaald vanuit het Grieks naar het Latijn door Willem van Moerbeke, wat lange tijd de basis vormde van wat in Europa bekend was van Over drijvende lichamen.

Stevin

Het zwaartepunt O en drukkingspunt L volgens Stevin in Vlietende Topswaerheyt uit 1605.

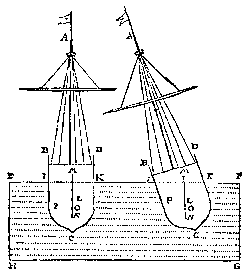
Bijna tweeduizend jaar na Archimedes zette Simon Stevin de volgende stap naar een stabiliteitstheorie. In 1586 werd De Beghinselen des Waterwichts uitgegeven in één band met De Beghinselen der Weeghconst, De Weeghdaet en een Anhang. Hierin behandelt hij onder andere de wet van Archimedes, de hydrostatische paradox en hydrostatische druk — zo'n tachtig jaar voordat Blaise Pascal zijn waarnemingen deed op het gebied van druk. Dit werk op het gebied van hydrostatica ging vooraf aan dat over stabiliteit. Dit behandelde hij als praktijkvoorbeeld in een supplement bij de heruitgave van Weeghconst uit 1605. In Vlietende Topswaerheyt bespreekt hij in twee bladzijden hoe hoog een aanvalsladder met krijgsvolk geplaatst kan worden, zonder dat het schip kapseist. Hierin stelt hij dat het waterhols swaerheyts middelpunt L (het drukkingspunt) in dezelfde verticale lijn moet liggen als het zwaartepunt O. Stevin nam uit onbekendheid met het begrip metacentrum foutief aan dat het zwaartepunt altijd onder het drukkingspunt moet liggen om een stabiel schip te verkrijgen. Stevin gaf echter al aan dat het bijzonder moeilijk is om het zwaartepunt van een schip vast te stellen, omdat dit uit zoveel onderdelen bestaat.

Hoste

Onder de invloed van vooral de Jezuïeten — die een bijzonder groot aandeel hadden in het onderwijs in Europa — werd echter nog lang vastgehouden aan de denkbeelden van Aristoteles. Zo gebruikte Paul Hoste nog in 1697 een combinatie van beide oude Grieken in zijn werk Théorie de la construction des vaisseaux. De opwaartse kracht baseerde hij op Archimedes, maar de hefboomwet baseerde hij op Aristoteles (hefboomarmen * snelheden zijn gelijk) in plaats van Archimedes (hefboomarmen * krachten zijn gelijk). Zijn werk was de eerste poging om de stabiliteit van een schip uit te drukken in wiskundige termen, al volgde uit zijn vergelijkingen dat als het zwaartepunt hoger komt te liggen, de stabiliteit verbetert in plaats van verslechtert. Hij stelde ook een praktische methode voor om de stabiliteit — of zoals hij het noemde, het vermogen om zeil te dragen — vast te stellen met een hellingproef, ook al maakte hij ook hier weer fouten in zijn afleidingen.

Bouguer en Euler

Metacentrum g volgens Pierre Bouguer in Traité du navire uit 1746.

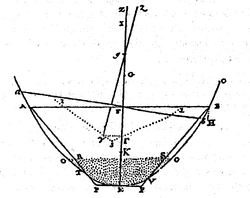
In 1746 publiceerde de Franse wiskundige Pierre Bouguer Traité du Navire. Hierin introduceerde hij het metacentrum M, het punt waar een schip rond slingert en waardoor de opwaartse kracht gaat. Daarnaast kwam hij met de juiste afleiding van de hellingproef.

Leonhard Euler maakte in Scientia Navalis uit 1749 gebruik van infinitesimaalrekening en definieerde het deplacement als de integraal van de hydrostatische drukverdeling over het natte oppervlak van een schip. Waar Bouguer uitging van het metacentrum als criterium van stabiliteit, ging Euler uit van het richtend moment dat ontstaat als resultaat van een veranderde resultante van de hydrostatische drukverdeling bij een schip dat een helling heeft. Euler berekende verder het oppervlaktetraagheidsmoment van de waterlijn, stelde de drie evenwichtsvoorwaarden voor drijvende lichamen op en bepaalde het moment van de in- en uittredende wiggen. Daniel Bernoulli definieerde het stabiliteitsmoment als product van de stabiliteitsarm en gewicht van het schip. Deze twee zijn de grondleggers van de hydrodynamica.

Fredrik Henrik af Chapman, scheepsbouwer van de Zweedse marine aan het einde van de achttiende eeuw, was de eerste die deze nieuwe kennis in de praktijk bracht. Zijn ontwerpen golden als de beste van die tijd. In 1768 kwam zijn boek Architectura Navalis Mercatoria uit, waarin al gesproken wordt over modeltesten in een bassin en wat al lijnenplannen bevat.

In 1798 publiceerde George Atwood A Disquisition on the Stability of Ships. Hierin kwam hij met de formule om de stabiliteit te berekenen bij grotere hellingen. Voor die tijd kon de aanvangsstabiliteit (stabiliteit bij rechtliggend schip) wel berekend worden. Er vergingen echter nog steeds schepen die bij grotere hellingen te weinig stabiliteit hadden, zoals de HMS Captain die kapseisde op 7 september 1870. Stabiliteitsberekeningen zijn sindsdien niet wezenlijk veranderd. Door de introductie van de computer is het echter niet meer de tijdrovende klus die het was.

Scheepsrampen zijn vaak de oorzaak van nieuwe wetgeving op het gebied van stabiliteit na lekraken. Het vergaan van het troepenschip HMS Birkenhead in 1852 bij Gansbaai in Zuid-Afrika waarbij 450 man verdronken, was de aanleiding tot nieuwe eisen in de Merchant Shipping Act van 1854. Na het vergaan van de Titanic in 1912 werd in 1913 de International Convention for the Safety of Life at Sea gehouden. De nieuwe inzichten werden echter pas toegepast na het vergaan van de Empress of Ireland in 1929 en hielden alleen rekening met de maximaal toelaatbare inzinking na lekraken en niet met de stabiliteit.

De International Load Line Convention van 1930 was een gevolg van de eerste internationale conferentie op het gebied. De afspraken die hier gemaakt werden, hadden te maken met reserve-drijfvermogen en daarmee werd het plimsollmerk wereldwijd aanvaard. Pas tijdens de International Load Line Convention van 1966 echter, werden voor het eerst echt eisen gesteld aan de stabiliteit en lekstabiliteit.

Om te kunnen blijven drijven, dient de opwaartse kracht op het lichaam gelijk te zijn aan het eigen gewicht. Om in dezelfde toestand te blijven liggen, dienen de opwaartse kracht en het gewicht boven elkaar te liggen. Het gewicht of deplacement Δ van het schip grijpt aan in G, het scheepszwaartepunt. De opwaartse kracht grijpt aan in B₀, het drukkingspunt.

Bij rechtliggend schip ligt het drukkingspunt in het vlak van kiel en stevens. Zodra het schip een helling krijgt, zal aan de ene zijde een deel van het schip onder water komen, de intredende wig. Aan de andere zijde zal een deel van het schip boven water uitkomen, de uittredende wig. Het geometrisch zwaartepunt verandert daardoor en het drukkingspunt verschuift evenwijdig aan de lijn g-g₁ naar de lage zijde.

Drukkingspunt B verplaatst bij veranderende hellingshoek. De baan van M is te construeren op de bovenstaande wijze, waarbij de kromming van de lijn van B overdreven is weergegeven.

Statische stabiliteit

De hierboven gegeven definitie geldt voor de statische stabiliteit. Hiervoor maakt men gebruik van de hydrostatica. Het houdt zich bezig met het schip in een bepaalde toestand, niet bewegend dus.

Opwaartse kracht

De wet van Archimedes luidt:

De opwaartse kracht die een lichaam in een vloeistof of gas ondervindt is even groot als het gewicht van de verplaatste vloeistof of gas.

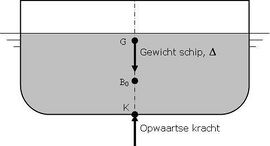
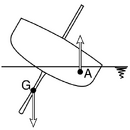
Om te kunnen blijven drijven, dient de opwaartse kracht op het lichaam gelijk te zijn aan het eigen gewicht. Om in dezelfde toestand te blijven liggen, dienen de opwaartse kracht en het gewicht boven elkaar te liggen. Het gewicht of deplacement Δ van het schip grijpt aan in G, het scheepszwaartepunt. De opwaartse kracht grijpt aan in B₀, het drukkingspunt. Dit is het meetkundig zwaartepunt van de waterverplaatsing.

Bij een volledig ondergedompeld lichaam valt het metacentrum samen met dit drukkingspunt. Wanneer een niet volledig ondergedompeld lichaam gedwongen wordt een hellingshoek ten opzichte van zijn evenwichtspositie te maken, dan verandert de vorm van het ondergedompelde lichaam en daarmee de positie van het drukkingspunt. Er wordt water verplaatst van de uittredende wig OLL₁ - het deel dat boven water komt - naar de intredende wig OWW₁ - het deel dat onder water komt. Van de intredende wig ligt het vormzwaartepunt in g, terwijl het vormzwaartepunt van de uittredende wig in g₁ ligt. Het geometrisch zwaartepunt verandert dus en het drukkingspunt B₀ verschuift evenwijdig aan de lijn g-g₁ naar de lage zijde naar B₁.

Door de verschuiving van het drukkingspunt naar de lage zijde verandert de richtende arm GZ en verbetert de stabiliteit ten opzichte van een volledig ondergedompeld lichaam. In de afbeelding is te zien dat de richtende arm de helling had vergroot als B in zijn oorspronkelijke positie was gebleven, maar nu een richtend koppel veroorzaakt.

Dwarsmetacentrum

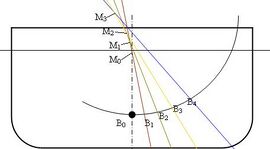
Het (dwars)metacentrum M is de snijding van de werklijnen van de opwaartse kracht bij hellingshoek φ van de opwaartse kracht met hellingshoek φ ± dφ. Als een schip een zekere hellingshoek krijgt, verandert de vorm van de carène. Hierdoor verplaatst B zich, waardoor ook de positie van M verandert.

M_φgrafiek. Bij kleine hoeken is M_φ vrijwel gelijk aan M₀. Bij grotere hoeken loopt M_φ uit het vlak van kiel en stevens tot het dek onder water loopt en de stabiliteit snel afneemt.

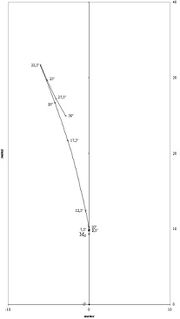
Zoals te zien, is M_φ bij kleine hellingshoeken vrijwel gelijk aan M₀. Voor hoeken kleiner dan 4° wordt voor conventionele schepen aangenomen dat M_φ gelijk is aan M₀. In de eerste figuur is punt K te zien. Dit punt ligt in het vlak van kiel en stevens. Voor een rechthoekige bak zou de afstand KB₀ op de helft van de diepgang liggen. Voor andere scheepsvormen geldt dit echter niet. Men kan B₀ uitrekenen door oppervlakteberekeningen van de waterlijn te maken. Bij een bepaalde diepgang T kan met behulp van het lijnenplan de oppervlakte van die waterlijn berekend worden met bijvoorbeeld de regel van Simpson. Door dit te doen bij meerdere diepgangen, kan met behulp van Bonjeankrommen voor elk van die diepgangen de KB₀ bepaald worden.

Nu moet nog de B₀M₀ bepaald worden. Dit gebeurt door het kwadratisch oppervlaktetraagheidsmoment I uit te rekenen. Af te leiden valt dat geldt:

<math>BM_{0}=\frac{I}{V}</math>

waarbij <math>I = \frac{ l \cdot b^3}{12} \,</math> (voor een rechthoekige bak). Hierbij geldt:
l = lengte schip
b = breedte schip
In deze formules is te zien dat vooral de breedte van invloed is op B₀M₀ en daarmee op de stabiliteit.

Uit de derde tekening is duidelijk dat:

KM₀ = KB₀ + B₀M₀

Deze gegevens worden aangeleverd door de scheepsbouwer en zijn aan boord beschikbaar. De KG moet voor elke reis bepaald worden. Het gewicht van eigen schip is bekend. De hoeveelheid en positie van de bunkers en ballast is te bepalen via tanktabellen. Het zwaartepunt van de lading zal vaak door de stuurman bepaald moeten worden. Met deze gegevens is via de momentenstelling KG uit te rekenen. Nu is de GM₀, de metacentrische hoogte, uit te rekenen met:

GM₀ = KM₀ - KG

Aanvangsstabiliteit

Vergelijking aanvangsstabiliteit

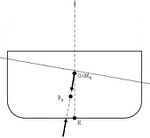
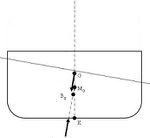
Richtend koppel, positieve aanvangsstabiliteit	Indifferente aanvangsstabiliteit	Kenterend koppel, negatieve aanvangsstabiliteit

De aanvangsstabiliteit gaat uit van een rechtliggend schip en is te zien in de onderstaande figuren. Zolang M₀ hoger ligt dan G zal het schip zich weer kunnen oprichten. Het schip heeft een positieve aanvangsstabiliteit, GM₀ = positief. Dit wordt een richtend koppel genoemd.
Als GM₀ = 0, dan wordt dit indifferente aanvangsstabiliteit, te zien in de middelste figuur.
Als GM₀ negatief is, spreekt men van een kenterend koppel, te zien in de rechtse figuur. Het schip heeft een negatieve aanvangsstabiliteit. GM₀ wordt de metacentrische hoogte genoemd. Voor de duidelijkheid is een grote hoek genomen, maar dit mag dus zoals gezegd tot ±5°.

In de figuur van het richtend koppel zijn Z en G' te zien. Z is de projectie van G parallel aan de waterlijn naar de lijn BM₀. G' is de dwarsscheepse projectie van G, parallel aan de deklijn, naar de lijn BM₀. Uit de tekening is op te maken dat GZ de richtende arm voorstelt. Voor kleine hoeken geldt bij benadering:

GZ = GM₀ * sinφ

Het moment van het richtend koppel is:

M = Δ * GZ = Δ * GM₀ * sinφ

Vergelijking begin- en eindstabiliteit

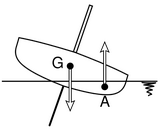
Vormstabiliteit, grote beginstabiliteit, lage eindstabiliteit	Gewichtsstabiliteit, lage beginstabiliteit, grote eindstabiliteit

Dit kan geschreven worden als:

M = Δ * KM₀ * sinφ - Δ * KG * sinφ

De eerste term, Δ * KM₀ * sinφ, is de vormstabiliteit, de tweede, Δ * KG * sinφ, is de gewichtsstabiliteit. De vormstabiliteit is alleen afhankelijk van de diepgang en de hellingshoek. De gewichtsstabiliteit is afhankelijk van de diepgang, hellingshoek en de gewichtsverdeling.

Hellingproef

De hellingproef, of stabiliteitsproef, houdt in dat men een bekend gewicht verplaatst aan boord. Door de verandering in hellingshoek te meten is de GM₀ te berekenen.

Grotere hellingen

Projectie van Mφ.

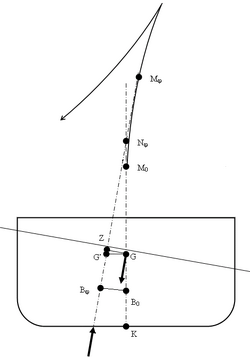
Zoals gezegd loopt M_φ uit het vlak van kiel en stevens bij grotere hellinghoeken. Om de berekeningen te vereenvoudigen, wordt het valse metacentrum geïntroduceerd, N. Dit is de projectie van M_φ op het vlak van kiel en stevens langs de werklijn van de opwaartse kracht. GZ is nu dus GN * sinφ, kortweg GNsinφ. De waarde van KNsinφ hangt alleen af van de helling en de diepgang. Deze worden door de scheepsbouwer uitgerekend en zijn aan boord beschikbaar als dwarskrommen. De waarde van KG is bekend van een bepaalde beladingstoestand, dus door voor verschillende hoeken de formule KG * sinφ in te vullen, kan bij deze hoeken de GZ uitgerekend worden, aangezien GN * sinφ = KN * sinφ - KG * sinφ.

<math>GNsin\varphi = KNsin\varphi - KGsin\varphi </math>

Stabiliteitskromme

Een stabiliteitskromme met de aanvangsstabiliteit GM₀ uitgezet bij 1 radiaal. De stabiliteit neemt aanvankelijk toe bij toenemende helling.

Stabiliteitskromme laag vrijboord. Bij toenemende helling neemt de stabiliteit ten opzichte van de aanvangsstabiliteit direct af.

Deze waarden kunnen worden uitgezet in een grafiek, de stabiliteitskromme, of GZ-kromme.

De aanvangsstabiliteit GM₀ is uitgezet bij 1 radiaal. Te zien is dat de kromme bij een kleine hellingshoek de GM₀-lijn volgt; M_φ ligt in het vlak van kiel en stevens. Ook te zien is dat de richtende arm in eerste instantie toeneemt bij een grotere helling. Dit komt doordat de waterlijn steeds breder wordt. Dit gaat steeds sneller tot het dek onder water raakt. Dit is het buigpunt, ook te zien als omslagpunt in de figuur Projectie van M_φ. Na dit buigpunt stijgt de arm nog wel, maar steeds minder snel, tot deze begint af te nemen. Het vrijboord is dus van grote invloed op het bereik van de stabiliteit. Als de arm af begint te nemen, is er nog wel een positieve arm, echter, als de kracht die de helling in eerste instantie veroorzaakte nog aanwezig is, dan zal het schip kapseizen.

Een speciaal geval was de Dongedijk, het schip dat op 15 augustus 2000 nabij Port Said kapseisde in gunstige weersomstandigheden. Doordat de havengelden in veel havens gekoppeld zijn aan de tonnenmaat - geen maat voor gewicht, zoals de naam doet vermoeden, maar voor het volume van een schip - worden er veel schepen ontworpen met een minimale vrijboord en veel lading aan dek. Groot tegenstander hiervan was ir. E. Vossnack, Oud-Hoofd Nieuwbouw Scheepsbouw Nedlloyd:

Ik heb mijn bedenkingen bij het hanteren van de tonnenmaat van schepen bij de afhandeling van vele financiële zaken. Hierdoor kunnen schepen worden ontworpen die naar mijn mening onvoldoende zeewaardig zijn. Bij de ’’Dongedijk’’ is dat naar mijn mening ook het geval. Ik zou er een voorstander van zijn dat er in internationaal verband, bijvoorbeeld geregeld door de IMO, van de tonnenmaat wordt afgestapt.

Duidelijk is dat een voldoende grote aanvangsstabiliteit niet garandeert dat de stabiliteit bij grotere hellingen voldoende is. Dit blijkt uit onderstaande grafiek, waar de GM₀ gelijk is aan de eerste GZ-kromme. Een laag vrijboord is hier in dit geval de oorzaak van.

Langsscheeps

Alle eerdergenoemde voorbeelden hadden betrekking op dwarsscheepse stabiliteit. Langsscheeps geldt hetzelfde. Echter, voor oppervlakteschepen is er in intacte toestand altijd voldoende langsscheepse stabiliteit, aangezien BM₀ zo groot is. Dit komt weer doordat I_y een grote waarde heeft. Het kwadratisch oppervlaktetraagheidsmoment neemt namelijk met de macht 3 toe naarmate de afstand tot het centrum toeneemt, zoals te zien is in de volgende formule: <math>BM_{0}=\frac{I_y}{V}</math>

waarbij <math>I_y = \frac{ b \cdot l^3}{12} \,</math>
Doordat de lengte van de meeste schepen veel groter is dan de breedte, is de langsscheepse stabiliteit intact vrijwel nooit een probleem.

Vrije vloeistofcorrectie

Vrije vloeistofcorrectie

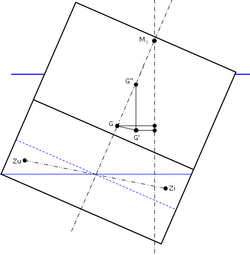
Tanks die niet volledig gevuld zijn, slacke tanks, hebben een nadelige invloed op de stabiliteit. Men spreekt dan over een vrij vloeistofoppervlak. Als een schip een helling krijgt, zal de vloeistof zich die kant op bewegen. Hierdoor krijgt het schip een grotere helling. In de stabiliteitsberekening dient men hier dus rekening mee te houden. Hoewel de gewichtsverplaatsing horizontaal is, wordt dit uitgedrukt als vermindering van de GM₀.

Volgens de zwaartepuntsverschuivingswet beweegt G zich evenwijdig aan de werklijn Z_u-Z_i naar G’. Denkbeeldig kunnen we G’ verschuiven naar G’’ over zijn werklijn naar het vlak van kiel en stevens. Nu is te zien dat dit leidt tot een schijnbare afname van de GM₀ met GG’’, de vrije vloeistofcorrectie (vvc). De gecorrigeerde metacentrische hoogte is:

G’M₀ = GM₀ - GG’’

GG’’ is uit te rekenen. Voor een rechthoekige tank kan de vvc berekend worden met:

<math>\frac{ l \cdot b^3 \cdot s.g.}{12 \cdot \Delta} \,</math>, waarin:

l = lengte van de tank
b = breedte van de tank
s.g. = soortelijk gewicht van de vloeistof
Δ = het gewicht van het schip
Uit de formule valt op te maken dat vooral de breedte van de tank van invloed is op de vvc. Om deze reden worden vaak langsschotten aangebracht in tanks. Door de scheepsbouwer wordt van elke tank de vvc berekend. Voor de stabiliteitsberekening zullen de vvc waarden van alle slacke tanks opgeteld worden.

Het effect van vrije vloeistof heeft al tot diverse rampen geleid, zoals met de European Gateway, de Herald of Free Enterprise en de Estonia. Vooral roll-on-roll-off-schepen lopen gevaar bij aanvaringen, door de grote ongedeelde dekken.

Dynamische stabiliteit

Dynamische stabiliteit is de arbeid die op een schip moet worden uitgeoefend om een zekere helling te verkrijgen. Het is een onderdeel van de hydrodynamica. Voor rotatie geldt de formule:

<math>W = M \cdot \varphi</math>

Omdat geldt:

<math>M = \Delta \cdot GNsin\varphi</math>

kan dit geschreven worden als:

<math>W = \Delta \cdot GNsin\varphi \cdot \varphi</math>

Als de stabiliteitskromme een rechthoekige vorm had, zou dit er als volgt uitzien:

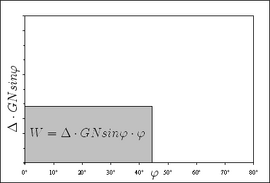
De y-as heeft hier niet dezelfde grootheid als de eerdere stabiliteitskrommen. Deze is vermenigvuldigd met Δ. Aangezien het deplacement constant is, verandert dit de vorm van de kromme niet. De werkelijke kromme is uiteraard niet rechthoekig. Aangezien deze kromme geen wiskundige betrekking heeft, wordt het gewenste oppervlak uitgerekend met de regel van Simpson.

Arbeid van kromme.

Als nu de grootheid op de y-as weer terug veranderd wordt naar GNsinφ, dan wordt niet de arbeid uitgerekend, maar de dynamische weg. Door het Schepenbesluit worden voor bepaalde schepen eisen gesteld aan de dynamische weg door middel van Bekendmaking aan de Scheepvaart No. 279/1992. Deze bekrachtigt IMO resolutie A.749(18), Code on Intact Stability for All Types of Ships Covered by IMO Instruments.

In BadS nr 279/1992 wordt onder andere de windeis genoemd. Hierin wordt gesteld dat een schip een helling verkrijgt van φ₀ onder invloed van een constante wind die een kracht uitoefent van 51,4 kgf/m². Rond deze hellingshoek slingert het schip met φ_A van loef naar lij. Als het zich in de uiterste loefstand bevindt en dan getroffen wordt door een windstoot met 1½ maal de kracht van de constante wind, mag de helling niet meer dan 50° bedragen, of minder als de stabiliteitsarm al eerder 0 is. Dit is uit te rekenen met behulp van de dynamische stabiliteit.

Slingertijd

De gevolgen van een kleine stabiliteit zijn duidelijk. Een te grote stabiliteit kan echter ook gevaar opleveren. Met een kleine stabiliteit slingert een schip verder door, maar wel langzamer. Een grote stabiliteit zorgt voor een snelle slingertijd, te vergelijken met een tuimelaar. De middelpuntvliedende kracht kan hierdoor zo groot worden dat verbanddelen van het schip te zwaar belast worden. Een ander gevaar is natuurlijk het schuiven van de lading. Eén en ander wordt duidelijk in de formule:

<math>T = \frac{2 \pi \cdot k_\varphi}{\sqrt{g \cdot GM}} = \sqrt{\frac{c \cdot b^2}{GM_0}} </math>

waarbij:
k_φ = de traagheidsstraal;
g = de valversnelling;
c = een ervaringsgetal, afhankelijk van de belading, ligt rond de ⁹/₁₆ s²/m;
b = breedte van het schip.
Een schip met grote stabiliteit wordt een wreed schip genoemd, met weinig stabiliteit een rank schip.

Lekstabiliteit

Bij alle voorgaande gevallen werd uitgegaan van een intact schip en daarmee van de intacte stabiliteit. Bij het ontwerp van een schip moet echter rekening gehouden worden met het eventueel lek raken van één of meerdere compartimenten door bijvoorbeeld een aanvaring. Bij het vervuld raken van een laadruim zou er voldoende reserve-drijfvermogen moeten zijn en voldoende lekstabiliteit. De scheepsbouwer moet voor elke mogelijkheid de overlevingskans uitrekenen, via de probabilistische lekberekening.

Door het lekraken verandert de carènevorm en daarmee de KM. Dat zou het moeilijk kunnen maken berekeningen te maken aan boord. Er zijn echter twee manieren om de nieuwe situatie te berekenen:

• verlies van drijfvermogen;
• laden van gewicht.

Er zijn twee verschillende mogelijkheden bij lekraken:

• het lekgeraakte deel van het schip is aan de bovenzijde begrensd;
• het lekgeraakte deel van het schip is aan de bovenzijde niet begrensd.

In het eerste geval kan worden gedaan alsof er een gewicht wordt geladen dat overeenkomt met het gewicht van het ingestroomde water. Dit gewicht hangt af van het volume van het compartiment. Als het een ruim betreft, kan dit leeg of geladen zijn. Als een ruimte geheel leeg zou zijn, zou het geheel vol kunnen stromen, als het volledig beladen is, kan er niets instromen. Dit wordt uitgedrukt in permeabiliteit, μ. Een geheel lege ruimte heeft een permeabiliteit van 0, geheel gevuld 1. Voor de machinekamer neemt men bijvoorbeeld aan, μ = 0,85.

In het tweede geval kan men deze methode ook gebruiken. Echter, als er gewicht geladen wordt, verandert de diepgang en eventueel trim en slagzij, waardoor er meer water en dus meer gewicht instroomt. Er zal dus meerdere keren moeten worden geïnterpoleerd. De berekening kan ook worden uitgevoerd door uit te gaan van het verlies van drijfvermogen. Nu moet worden bepaald wat de verloren waterlijn is. In moderne stabiliteitsprogramma's is dit voor de belangrijkste compartimenten bekend.

Vergelijking onderzeeboot boven en onder water met oppervlakteschip

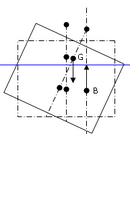
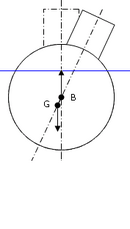
Onderzeeboot onder water	Oppervlakteschip	Onderzeeboot boven water

GZ-krommen

Bijzondere gevallen

Onderzeeboten

Onderzeeboten die zich geheel onder water bevinden hebben geen waterlijn. Hierdoor vervalt de BM-component. Het zwaartepunt G moet zich dus, in tegenstelling tot oppervlakteschepen, onder drukkingspunt B bevinden om een positieve stabiliteit te hebben.

Een ander probleem wordt veroorzaakt door de ronde vorm. Deze is vereist om voldoende weerstand tegen de waterdruk te bieden op grote diepte. Hierdoor wordt boven water de waterlijn niet groter bij een helling, zoals bij oppervlakteschepen, zoals in de figuren links te zien is. Echter, doordat B lager ligt dan G neemt het richtend koppel toe bij groter wordende helling. Onderwater ligt het maximale richtende koppel bij 90°, boven water iets eerder. Doordat BM wegvalt, is onder water de langscheepse stabiliteit gelijk aan de dwarscheepse stabiliteit, aangezien KB geldt voor de gehele carène. Dit afgezien van de vrije vloeistofcorrectie.

Verder hebben onderzeeboten onder water een neutraal drijfvermogen; anders zouden ze zinken of aan de oppervlakte komen. De hoofd-ballasttanks worden onder water geheel gevuld, om het effect van het vrije vloeistof oppervlak te verminderen. Eventuele correcties aan de ballast - om te vertrimmen, of om extra gewicht te compenseren - wordt gedaan met hulp-ballasttanks. Aangezien de capaciteit van deze ballasttanks beperkt is, is het belangrijk om een bepaald gewicht niet te overschrijden. Vertrimmen kan gebeuren met behulp van ballast, maar ook door gebruik te maken van duikroeren. Dit laatste kan alleen als de onderzeeboot vaart loopt.

Als een onderzeeboot tot grote diepte duikt, zal deze onder invloed van de waterdruk enigszins in elkaar gedrukt worden. Het volume neemt af, waardoor de opwaartse druk afneemt. Het soortelijk gewicht van het water neemt wel toe door de hogere druk en het hogere zoutgehalte op grotere diepte, maar dit is niet voldoende om de vermindering van volume te compenseren.

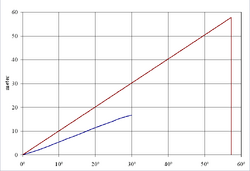
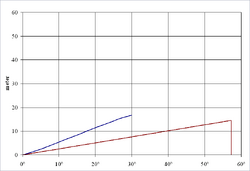
In de figuur hiernaast is het verschil te zien tussen de GZ-krommen. Duidelijk te zien is dat de stabiliteit van een oppervlakteschip groter is dan die van een onderzeeboot. Echter, bij een bepaalde helling raakt het dek van een oppervlakteschip onder water en verliest het stabiliteit. Daar komt nog bij dat er bij een bepaalde helling, Ф_f, openingen onder water raken, waardoor er water in het schip komt. Een onderzeeboot heeft hier geen last van en heeft zelfs ondersteboven nog een richtend koppel.

Half-afzinkbare schepen

Vergelijking aanvangsstabiliteit en stabiliteitkrommes

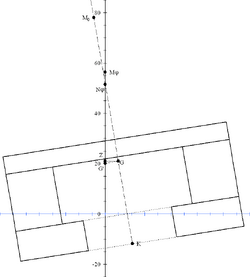
Helling bij 66.480 ton	Helling bij 66.481 ton
GZ-kromme bij 66.480 ton	GZ-kromme bij 66.481 ton

Bij half-afzinkbare schepen treedt er bij rechtliggend afzinken een plotselinge verandering van KM₀ op zodra de drijvers, of de pontons, onder water komen. De waterlijn, waar BM₀ van afhankelijk is, vermindert immers. Om deze reden zinken veel semi-subs altijd met een zekere trim af. Hierdoor verandert de waterlijn geleidelijk en de GM_φ dus ook. Dit is een zeer duidelijk voorbeeld van het verschil tussen GM₀ en GM_φ.

Hiernaast is als voorbeeld een vooraanzicht van de Balder te zien op. De pontons verdwijnen bij rechtliggend schip bij 12 meter onder water. Dit is bij een deplacement van 66.481 ton. Op de plaatjes links is het deplacement 66.480 ton, rechts 66.481 ton. Voor de duidelijkheid is de helling ruim 9°, een extreme waarde voor dit type schepen.

Duidelijk te zien is de enorme afname van G’M₀. Dit is logisch; dit is de metacentrische hoogte voor een rechtliggend schip. Bij een rechtliggend schip treedt er bij het inzinken van de pontons een enorme afname van de wateroppervlakte op. Als het schip een helling heeft, treedt die verandering niet op, zoals duidelijk te zien is. De G’M_φ verandert dus niet. Als men zou rekenen met de G’M₀ in plaats van de G’M_φ, dan zou de helling links veel kleiner zijn en rechts veel groter.

Zoals te zien neemt de G’M₀ enorm af, zodra de pontons onder water zijn. Voor hijsoperaties is echter een grote stabiliteit vereist. Dit heeft men opgelost door de kolommen ver uit het centrum te plaatsen. Wateroppervlakte in het centrum heeft minder invloed op BM₀ dan wateroppervlakte verder naar buiten. Er geldt:

<math>BM_0 = {\frac {I}{V}}</math>

Hierbij geldt voor <math>I = 2 \cdot \int_{x=0}^{x=L} \frac{1}{3} y^3 \cdot {\rm d}x</math> waarbij:
L = lengte schip
y = afstand van oppervlakte waterlijn tot aan het vlak van kiel en stevens
dx = een infinitesimaal klein stukje van de x-as, waar het vlak van kiel en stevens de waterlijn snijdt
Doordat I toeneemt met de macht drie als de kolommen verder uit elkaar geplaatst worden, is er een zeer grote stabiliteit te bereiken.

Sleepboten

Voor sleepboten kan de stabiliteit in gevaar komen tijdens slepen. Tijdens manoeuvreren kan de draad over een van de boorden lopen in plaats van naar achteren. Indien er dan een te grote kracht op komt, bestaat het gevaar van kapseizen. Dit was een van de oorzaken van het kapseizen van de Deense AHT Stevns Power, op 19 oktober 2003 bij Nigeria, waarbij alle 11 bemanningsleden omkwamen.

Wetgeving

Door de wetgever worden een aantal eisen gesteld aan een schip, voordat het aan de reis mag beginnen. Dit verschilt enigszins per type schip. Vrij algemeen echter geldt:

• minimum metacentrumhoogte:
  • G’M₀ 0,15 meter voor vrachtschepen;
  • G’M₀ 0,50 meter voor zeilschepen;
  • G’M₀ 0,30 meter voor vrachtschepen geladen met graan in bulk;
  • G’M₀ 0,10 meter voor vrachtschepen met deklading hout, waaraan drijfvermogen kan worden ontleend;
• GZ bedraagt bij 30° minimaal 0,20 meter;
• top van de GZ-kromme bij minstens 30°;
• oppervlak onder de GZ-kromme, de dynamische weg, tot 30° 0,055 mrad;
• oppervlak onder de GZ-kromme tot 40° (of de hellingshoek waarbij het schip vervuld raakt,Ф_f) 0,09 mrad;
• oppervlak onder de GZ-kromme tussen 30 en 40° (of Ф_f) 0,03 mrad;
• de maximale waarde van de armen van statische stabiliteit wordt bij voorkeur bereikt bij een helling van ten minste 30°, doch in geen geval bij een helling van minder dan 25°.

Veel wetgeving wordt internationaal geregeld via de IMO of de EG, waarna het bekrachtigd wordt in lokale wetgeving:

• Bekendmaking aan de Scheepvaart nr. 255/1990: Intacte stabiliteit van pontons, bestemd voor het vervoer van dekladingen;

Strekt ter uitvoering van circulaire MSC/Circ. 503, Intact stability requirements for Pontoons, van de Maritieme Veiligheidscommissie van de IMO;

• Bekendmaking aan de Scheepvaart nr. 279/1992: Stabiliteit van schepen in intacte toestand, geen offshore bevoorradingsschepen of onbemande pontons voor vervoer van deklading zijnde;

Geeft uitvoering aan resoluties A.167(ES IV), A.206(VII) en A.562(14) van de Algemene Vergadering van de IMO;

• • A.167(ES IV), Recommendation on intact stability for passenger and cargo ships under 100 metres in length;
  • A.206(VII), Recommendation for an interim simplified criterion for decked fishing vessels under 30 metres in length;
  • A.562(14), Recommendation on a severe wind and rolling criterion (weather criterion) for the intact stability of passenger and cargo ships of 24 metres in length and over;

All are superseded by

• • • A.749(18) Code on Intact Stability for All Types of Ships Covered by IMO Instruments;
• Bekendmaking aan de Scheepvaart nr. 280/1992: Voorschriften voor de waterdichte afsluiting, de stabiliteit en de waterdichte indeling van offshore bevoorradingsschepen;
• richtlijn 98/18/EG van de Raad van de Europese Unie inzake veiligheidsvoorschriften en -normen voor passagiersschepen;
• richtlijn 2003/25/EG van de Raad van de Europese Unie inzake specifieke stabiliteitsvereisten voor roropassagiersschepen;
• MODU-Code 1989, Code for the Construction and Equipment of Mobile Offshore Drilling Units

Definities

Hieronder volgen enige definities die gebruikt worden in stabiliteit. De Engelstalige definities verschillen iets van de Nederlandstalige, maar worden internationaal meer gebruikt.

Stabiliteitstermen
Term	Afkorting	Engelse term	Afkorting
Deplacement Kiel Drukkingspunt Zwaartepunt Metacentrum Hoogte kiel-drukkingspunt Hoogte kiel-zwaartepunt Hoogte kiel-metacentrum Hoogte metacentrum Lengte tussen de loodlijnen Lengte over alles Langsscheepse ligging B Langsscheepse ligging G Langsscheepse ligging kantelpunt Dwarsscheepse ligging B Dwarsscheepse ligging G Dwarsscheepse ligging kantelpunt Stabiliteitsarm, richtende arm of arm van statische stabiliteit	Δ K B G M KB KG KM GM Lll Loa Xb Xg Xa Yb Yg Ya GZ	Displacement Keel Centre of buoyancy Centre of gravity Metacentre Vertical centre of buoyancy Vertical centre of gravity Height metacenter above the Keel Metacentric height Length between perpendiculars Length over all Longitudinal centre of buoyancy Longitudinal centre of gravity Longitudinal centre of flotation = tipping centre Transverse centre of buoyancy Transverse centre of gravity Transverse centre of flotation Righting arm	Δ K B G M VCB VCG KM GM Lpp Loa LCB LCG LCF   TCB TCG TCF GZ

Langsscheepse stabiliteits-termen.

Literatuur

• Chapman, F.H. af (2006): Architectura Navalis Mercatoria: The Classic of Eighteenth-Century Naval Architecture, Dover Publications, Mineola, N.Y.,
• Dokkum, K. van, Katen, H. ten (2007): Scheepsstabiliteit, Dokmar, Enkhuizen,
• Ferreiro, L.D. (2006): Ships and Science: The Birth of Naval Architecture in the Scientific Revolution, 1600-1800 (Transformations: Studies in the History of Science and Technology), The MIT Press, Cambridge, Mass.,
• Glas, K., Schutte, J.W. (1984): Zeemanschap voor de handelsvaart, deel 2, Educaboek/Stam Technische Boeken, Culemborg,
• Metzlar K. (1990): Stabiliteit van Schepen, Smit en Wytzes, Urk.

Noten

Wikibooks

Wikibooks heeft meer over dit onderwerp: Scheepsstabiliteit.