Geografische coördinaten
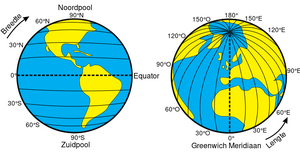

Geografische coördinaten zijn coördinaten waarmee een locatie op aarde numeriek wordt vastgelegd met breedtegraad, lengtegraad en eventueel hoogte. Dergelijke geografische coördinaten zijn gebaseerd op een geodetisch coördinatensysteem zoals het International Terrestrial Reference System.
Beschrijving
De isolijnen van geografische coördinaten vormen een denkbeeldig net. De noord-zuidlijnen, die van pool tot pool lopen, worden meridianen genoemd. De oost-westlijnen worden parallellen (of breedtecirkels) genoemd en zijn evenwijdig met de evenaar.
Bepaling
Vanouds werd in de zeevaart de breedtegraad bepaald door de hoogte van hemellichamen op te nemen. De afstand in graden tot de evenaar, gemeten langs een meridiaan, is namelijk gelijk aan de hoek van de Poolster met de horizon, de poolshoogte.
De lengtegraad (ooster- of westerlengte) van een plaats is de hoek tussen de meridiaan van die plaats en de nulmeridiaan (sinds 1884 de meridiaan van Greenwich). De lengtegraad kon pas nauwkeurig bepaald worden met de ontwikkeling van nauwkeurige klokken.
Om op zee de lengte te bepalen, werd het tijdstip waarop de zon op haar hoogste punt stond afgelezen op een chronometer die gelijk was gezet aan de tijd van Greenwich (of een ander punt). Een verschil van een uur (een 24e deel van een dag) komt overeen met een verschil in geografische lengte van 15 graden (een 24e deel van een cirkel). Een afwijking van 1 seconde op de chronometer resulteert in een positiefout van 15 boogseconden (464 m op de evenaar). Hieruit blijkt dat er onderscheid moet worden gemaakt tussen enerzijds minuut en seconde op de klok en anderzijds de boogminuut en boogseconde in geografische coördinaten.
Notatie
Geografische posities worden traditioneel uitgedrukt in booggraden (°), onderverdeeld in 60 minuten (') en 60 seconden ("), dus ddd°mm'ss,s". Men werkt ook wel met decimaal onderverdeelde minuten (ddd°mm,mmm') of decimaal onderverdeelde graden (ddd,dddd°).
Traditioneel wordt eerst de noorderbreedte (NB) of zuiderbreedte (ZB) en daarna de oosterlengte (OL) of westerlengte (WL) vermeld.
Afstanden berekenen
Tegenwoordig wordt ook veel met geprojecteerde coördinaten gewerkt. Deze bestaan uit een rechthoekig rooster van kilometers. Er zijn nationale geprojecteerde coördinaten, zoals de Nederlandse Rijksdriehoeksmeting, regionale, en wereldwijde, zoals UTM. Om de geografische coördinaten om te rekenen moet men er rekening mee houden dat de vorm van de aarde een ellipsoïde is.
Latitudinale afstanden
De latitudinale afstand in meters voor 1° varieert vanwege de afplatting van de aarde enigszins met de geografische breedte <math>\varphi</math>. Een benadering is:[1]
- <math>\mathrm{dist}(\varphi) = 111\,132{,}954 - 559{,}822\,\cos(2\,\varphi) + 1{,}175\,\cos (4\,\varphi)</math>
Longitudinale afstanden
De longitudinale afstand voor 1° neemt heel sterk af als functie van de geografische breedte φ doordat alle meridianen samenlopen aan de noord- en zuidpool. De afwijkingen nemen heel sterk toe voor de hogere breedtes.
Veronderstel de aarde als een bol:
- <math>dist_x = M_r \, \frac{\pi}{180} \, \cos (\varphi)</math>
Beschouw de aarde als een ellipsoïde:
- <math>\tan (\beta) = \frac{b}{a} \, \tan (\varphi)</math>
- <math>dist_x = a \, \frac{\pi}{180} \, \cos (\beta)</math>
Referentie: WGS 84 geodetisch datum
- <math>M_r</math> = 6 367 449 m (gemiddelde aardstraal)
- <math>\varphi</math> = latitude
- <math>\beta</math> = gereduceerde latitude
- <math>\frac{b}{a}</math> = 0,996 647 19 (verhouding poolstraal / equatoriale aardstraal)
- <math>a</math> = 6 378 137 m (equatoriale aardstraal)
| Latitude (°) | Latitudinale afstand voor 1° (km) |
Longitudinale afstand voor 1° bij een bol (km) |
Longitudinale afstand voor 1° bij een ellipsoïde (km) |
Locatie |
|---|---|---|---|---|
| 52°NB | 111,267 | 68,420 | 68,678 | Delft - Gouda - Nieuwegein - Veenendaal - Arnhem[2] |
| 51°NB 1 | 111,248 | 69,938 | 70,198 | Diksmuide - Gent - Dendermonde - Mechelen - Aarschot - Diest - Lummen |
| 50°NB 1 | 111,229 | 71,435 | 71,696 2 | Gedinne - Saint-Hubert - Bastenaken |
| 49°NB | 111,210 | 72,910 | 73,172 | Parijs - Verdun - Metz |
| 0°NB | 110,574 | 111,1333 | 111,320 3 | Equator |
Noten:
- 49°50'NB en 51°10'NB is de basis van de Lambert 2008-projectie. Het latitudinale verschil voor 1° tussen deze breedtegraden is minder dan 20 m.
- Bemerk dat er ca. 1500 m longitudinaal verschil is voor 1° tussen 50°NB en 51°NB.
- De zeemijl is 1852 m zodat deze overeenkomt met 1/60ste breedtegraad. Aangezien 1852 × 60 = 111 120 m, is een zeemijl aan de evenaar net iets meer dan 1' en op de polen juist minder.
Zie ook
- Geodetisch coördinatensysteem
- Cartesisch coördinatenstelsel
- Rijksdriehoekscoördinaten (Nederland)
- Lambertcoördinaten (België)
- Globe
- ↑ (en) Understanding terms in Length of Degree formula?. Geographic Information Systems StackExchange (25 oktober 2013). Gearchiveerd op 13 juli 2022. Geraadpleegd op 13 juli 2022.
- ↑ Zie bijvoorbeeld de ProRail Spoorkaart 2020, waarop RD- en geografische coördinaten zijn aangegeven
