Hoek (meetkunde)

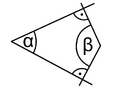
Een hoek in de meetkunde is een figuur in een vlak gevormd door twee lijnstukken of daar het verlengde van, van halve lijnen met een gemeenschappelijk beginpunt, het hoekpunt. De twee lijnen die de hoek bepalen worden de benen van de hoek genoemd. Hoek wordt ook gebruikt voor de grootte van een draaiing.

In het geval van een draaiing betreft het een draaiing van een van de benen om het hoekpunt tot die met het andere been samenvalt. Deze beweging kan op twee manieren plaatsvinden, zodat door de halfrechten ook twee hoeken worden gevormd. Men rekent zonder nadere bepaling meestal de kleinste van beide hoeken als de hoek gevormd door de twee lijnen. De hoek tussen twee lijnen is dan maximaal een rechte hoek.

Bij een veelhoek gaat het zonder nadere aanduiding om de binnenhoek, ook als die niet de kleinste van de twee is. Bij vectoren is de hoek maximaal een gestrekte hoek.

Een hoek is een dimensieloze grootheid, waarvan de grootte traditioneel in graden, maar in de exacte wetenschap en het SI-stelsel in radialen wordt uitgedrukt. Hoeken worden in het SI-stelsel met radialen aangegeven, maar het gebruik van graden is voor officieel gebruik toegestaan.

Het snijpunt van de twee lijnen wordt wel hoekpunt genoemd.

Geschiedenis

Hoeken werden reeds bij de Babyloniërs, die van 4000 tot 300 v.Chr. leefden, bestudeerd in de astronomie en de bouwkunde. De Babyloniërs gebruikten een sexagesimaal talstelsel. Toenmalige wiskundigen verdeelden de cirkel in zes maal 60 eenheden, die dus overeenkwamen met de graden van nu. De graad werd later verder opgesplitst in 60 minuten, ook wel boogminuten genoemd ter onderscheid van de minuut in tijd, en de minuut in 60 seconden of boogseconden. ^[1]

De oude Grieken breidden de kennis over hoeken verder uit. Eratosthenes wist aan de hand van hoekverschillen de omtrek van de Aarde te bepalen. Pythagoras toonde aan dat de som van de hoeken in een driehoek 180° is.

Al-Jayyani (989 - 1079) schreef het eerste werk over boldriehoeken en Snellius beschreef in 1617 de eerste driehoeksmeting met een keten van driehoeken om de omtrek van de Aarde te bepalen. Hij ontdekte in 1621 de wet van Snellius: hoe de invalshoek van licht verandert op de overgang van het ene medium naar het andere, zoals tussen lucht en water.

Tekenen van een hoek

Een van de drie klassieke problemen van de Grieken was de driedeling van een hoek met alleen passer en liniaal. Het was hun wel al gelukt een hoek in tweeën te delen en te verdubbelen, hoeken op te tellen en af te trekken, en bepaalde hoeken, onder andere van 54°, 60°, 72° en 90°, te tekenen. De constructie van een hoek van 54° gaat via een regelmatige drie- en vijfhoek. Daaruit kon een groot arsenaal afgeleide hoeken worden bepaald, maar niet alle hoeken. Pas in 1837 werd door Pierre Wantzel aangetoond dat de driedeling niet mogelijk is.

Het blijkt dat alleen hoeken, die een veelvoud van drie graden zijn, met passer en liniaal kunnen worden geconstrueerd.

Eenheden

Hoeken worden gebruikelijk in graden uitgedrukt. Graad is de afkorting van booggraad, maar in het algemeen wordt het tot graad afgekort. Het symbool voor een graad is °. Een hoek met een grootte van een hele cirkel telt voor 360°. Twee lijnstukken in elkaars verlengde vormen een hoek van een halve cirkel, dus van 180°. Staan de lijnstukken loodrecht op elkaar, dan is de hoek tussen beide 90°. Een graad wordt traditioneel onderverdeeld in 60 boogminuten of meestal minuten, symbool ', en een minuut weer in 60 boogseconden of seconden met symbool ". Als nog verdere onderverdeling nodig is worden cijfers achter de komma gebruikt bij de seconden. Een hoek van 34 graden, 25 minuten en 16,5 seconden wordt genoteerd als: 34°25'16,5".

Bij het meten van hoeken in radialen speelt het getal π een belangrijke rol. Zo is een cirkel gelijk aan <math>2 \pi</math> radialen.

De SI-eenheid waarin een hoek wordt gemeten is de radiaal (rad).

Een rechte hoek is gelijk aan <math>\tfrac 12 \pi</math> rad.
Een cirkel omvat <math>2 \pi</math> rad.

De meeteenheid graad (°) is in het dagelijks leven gebruikelijker.

Een rechte hoek is 90°.
Een cirkel omvat 360°.

In de landmeetkunde wordt de decimale graad of gon gebruikt.

Een rechte hoek meet 100 gon.
Een cirkel omvat 400 gon.

De hoek van een helling wordt, bijvoorbeeld op verkeersborden, vaak aangegeven in procenten. Die is doorgaans gelijk aan de tangens van de hellingshoek, soms de sinus, uitgedrukt in procenten. Voor kleine hoeken zijn zowel de tangens als de sinus met goede benadering gelijk aan de hoek zelf, uitgedrukt in radialen.

In het leger wordt de volledige cirkel opgedeeld in 6300 of 6400 eenheden, mil genaamd. Deze van de radiaal afgeleide eenheid is eenvoudig te gebruiken bij het inschieten van artillerie, als een schot een doel op 1000 meter met 5 meter mist kan het stuk 5 mil worden gedraaid.

Conversies tussen de verschillende eenheden

2π rad = 360° = 400 gon

1 rad ≈ 57° 17' 44,8" ≈ 57,2958° ≈ 63,6620 gon
1° ≈ 0,017453 rad ≈ 1,1111 gon
1 gon = 0° 54' = 0,9° ≈ 0,015708 rad

Conventies

Een hoek is in de wiskunde positief indien deze in tegenwijzerzin wordt gelezen en negatief indien deze in wijzerzin wordt afgelezen. Men spreekt dan van gerichte hoeken.

In volgende figuur is <math>\angle{CAB} = - \angle{BAC}</math>. Hoek <math>\angle{BAC}</math> is positief, hoek <math>\angle{CAB}</math> is negatief.

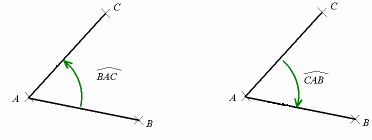
Dit is in de landmeetkunde precies andersom. Bij een linkshandig coördinatensysteem, zoals dat van een computerbeeldscherm of -printer waar de positieve <math>y</math>-as naar beneden wijst, zijn hoeken met de klok mee ook positief.

De hoek tussen twee lijnen wordt gegeven als gerichte hoek en is dan goed gedefinieerd 'modulo' <math>\pi</math>.
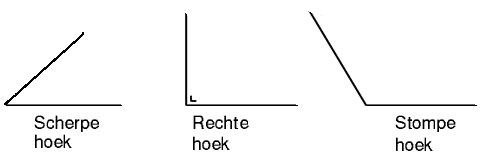
Een hoek van 90° of <math>\frac{\pi}{2}</math> wordt recht genoemd, een hoek die kleiner is, is een scherpe hoek, een hoek die groter is, is stomp. Een rechte hoek wordt ook wel haaks genoemd, een hoek van 180° of <math>\pi</math> een gestrekte hoek.

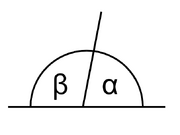
Complementaire en supplementaire hoeken

<math>\alpha</math> en <math>\beta</math> zijn supplementaire hoeken, de ene is het supplement van de andere, als de som van de twee hoeken een gestrekte hoek is, wiskundig: <math>\alpha + \beta = \pi</math> of 180°.

<math>\alpha</math> en <math>\beta</math> zijn complementaire hoeken, de ene is het complement van de andere, als de som van de twee hoeken een rechte hoek is, wiskundig: <math>\alpha + \beta =\frac{\pi}{2}</math> of 90°.


Supplementaire hoeken	Complementaire hoeken

1/60 van een graad (°) is een boogminuut (1'), 1/60 van een boogminuut is een boogseconde (1")
Hoeken blijven gelijk wanneer er een geheel keer 2π, dus een hoek in radialen, of 360°, in graden, bij wordt opgeteld. De hoofdwaarde van een hoek is de grootte van de hoek <math>\theta</math>, zodat <math>0 \leq \theta<2\pi</math>, wanneer <math>\theta</math> in radialen is gegeven, of zodat <math>0\leq \theta<360^\circ</math>, in graden.

Eigenschappen

Gelijke hoeken

In de drie hieronder staande gevallen is <math>\alpha = \beta</math>:

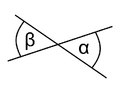
	overstaande hoeken
	Hier is de lijn <math>h</math> evenwijdig aan <math>h'</math>.
	Opnieuw is <math>h</math> evenwijdig aan <math>h'</math>, dit geval is uit de bovenstaande twee te halen.

Het gaat bij de laatste twee voorbeelden om F- en Z-hoeken. Hieronder zijn de rechte hoeken (<math>\frac{\pi}{2}</math> rad) aangeduid met een boog en een punt:

	hier is <math>\alpha = \beta</math>
	hier is <math>\alpha + \beta =\pi</math>

Overstaande hoeken

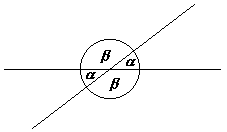
Wanneer twee lijnen in een vlak elkaar snijden, worden door deze lijnen vier hoeken gevormd. De overstaande hoeken zijn daarbij in grootte aan elkaar gelijk. Twee aangrenzende hoeken zijn samen 180° en de vier hoeken, die door de twee lijnen worden bepaald, vormen samen een cirkel. De hoek tussen twee lijnen kan op twee manieren worden gemeten. Meestal, maar niet noodzakelijk, wordt onder de hoek de kleinste hoek verstaan, in dit geval hoek <math>\alpha</math>.

Hoeken in regelmatige veelhoeken

In het euclidische vlak geldt dat de som van de hoeken van een driehoek 180° (<math>\pi</math> rad) is, bij een vierhoek is de som 360° (<math>2\pi</math> rad).

Algemeen geldt voor een veelhoek met <math>n</math> zijden, dat de som van de inwendige hoeken <math>(n-2) \pi</math> of <math>(n-2) \times 180^\circ</math> is.

Op die manier kan worden afgeleid, dat de hoeken in een gelijkzijdige driehoek 60° of <math>\frac{\pi}{3} \text{rad}</math> is en in een vierkant 90° of <math>\frac{\pi}{2} \text{rad}</math>.

Meer algemeen: de hoeken van een regelmatige n-hoek zijn elk <math>\frac{n-2}{n} \times 180^\circ</math> oftewel <math>\frac{n-2}{n} \pi</math> rad.

Hoeken tussen vlakken

Hoeken worden in het platte vlak gemeten. Wanneer twee vlakken <math>V</math> en <math>W</math> elkaar snijden, dus er een lijn is die door beide vlakken gaat, hun snijlijn, wordt de mate waarin het ene vlak moet roteren om die lijn, om samen te vallen met het andere, de hoek tussen deze vlakken genoemd. De hoek wordt dan in het vlak gemeten, dat loodrecht op <math>V</math> en <math>W</math> staat.

Bepalen van een hoek

Meten

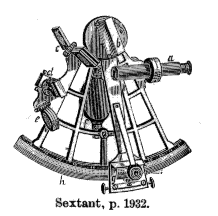
Een hoek kan rechtstreeks of als het verschil van twee richtingen gemeten worden met een:

gradenboog op een geodriehoek of kaarthoekmeter, bijvoorbeeld voor een hoek op papier,
goniometer voor de hoek tussen kristalvlakken,
hoekmeter, bijvoorbeeld voor de hoek lussen twee houten balken,
inclinometer, bijvoorbeeld voor een verticale hoek van een dakbalk of een berghelling,
sextant voor het bepalen van horizontale en verticale hoeken voor navigatie,
richtkompas, mechanisch of elektronisch, voor een horizontale hoek op land of zee,
gyroscoop voor 3D rotaties van bijvoorbeeld schepen en vliegtuigen,
rotatiesensor op basis van versnellingsmeters zoals bijvoorbeeld in een smartphone,
landmeetkundig waterpasinstrument met gradenrand voor een horizontale hoek in het terrein of
total station of ouder landmeetkundig instrument zoals jakobsstaf, theodoliet, of tachymeter voor het afzonderlijk bepalen van een horizontale en een verticale hoek.

Berekenen

Een hoek kan ook worden berekend, bijvoorbeeld uit met een liniaal gemeten afstanden of met satellietnavigatie bepaalde coördinaten. De hoek tussen twee wiskundig beschreven lijnen of vlakken kan in een hoek tussen twee vectoren worden omgezet.

De hoek <math>\theta</math> tussen twee vectoren <math>\mathbf{u}</math> en <math>\mathbf{v}</math> kan worden berekend met:

<math>\cos(\theta) = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\|\ \|\mathbf{v}\|}</math>

Waarbij gebruik gemaakt wordt van het inwendige product. Dit geldt meer algemeen in iedere inwendig-productruimte.

Het kan ook met:

<math>\sin(\theta) = \frac{\mathbf{u} \times \mathbf{v}}{\|\mathbf{u}\|\ \|\mathbf{v}\|} </math>

waarbij van het kruisproduct gebruik wordt gemaakt.

Voorbeelden van het omzetten naar een hoek tussen twee vectoren:

De hoek tussen twee lijnen wordt berekend uit richtingsvectoren van beide lijnen.
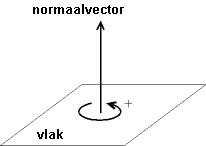
De hoek tussen twee vlakken wordt berekend uit de hoek tussen normaalvectoren van de vlakken.
De hoek <math>\theta</math> tussen een vlak en een lijn wordt berekend uit het complement van de hoek <math>\alpha</math> tussen een normaalvector op het vlak en een richtingsvector van de lijn:

<math>\theta = 90^\circ-\alpha =\frac{\pi}{2}\ \text{rad}-\alpha</math>

De hoek tussen twee snijdende lijnen in een meerdimensionale ruimte is de hoek in het vlak van de twee lijnen.

Riemann-meetkunde

In de niet-Euclidische elliptische meetkunde van Bernhard Riemann die onder meer wordt toegepast in de algemene relativiteitstheorie wordt de metrische tensor gebruikt om de hoek tussen twee raaklijnen te bepalen. Met U en V raakvectoren en g<sub### {gte:0} not found ###ij< sub=""> de komponenten van de metrische tensor G krijgen we voor de onderlinge hoek

<math>

\cos \theta = \frac{g_{ij}U^iV^j} {\sqrt{ \left| g_{ij}U^iU^j \right| \left| g_{ij}V^iV^j \right|}}. </math>

Gebruik

Een greep uit de talloze toepassingen:

in de wiskunde (meetkunde):
- coördinatenstelsels zoals poolcoördinaten en bolcoördinaten
- hoeken van Euler
in de geodesie (aardrijkskunde):
- azimut
- lengte- en breedtegraad
in de sterrenkunde
- de definitie van de parsec: De parsec is de afstand die men vanaf de Aarde de ruimte moet ingaan, opdat men van die afstand de gemiddelde afstand Aarde -zon onder een hoek van één boogseconde ziet (zie figuur).
- de afbuiging van licht bij een zware massa: zie zwaartekrachtlens

in de optica (natuurkunde)
- invalshoek: hoek tussen de invallende stralen en de normaal op het scheidingsvlak tussen twee middenstoffen
- parallax
- hoek van diffractie bij een (reflectie)tralie.
in de aerodynamica: de invalshoek is de hoek waarlangs het fluïdum het vleugelprofiel treft
bij de scheepsbewegingen van schepen en vliegtuigen: rol-, gier- en stamphoeken

Verhouding tussen hoek, tijd en afstand op Aarde

Onderstaande tabel geeft de verhouding tussen de hoek vanuit het massamiddelpunt van de Aarde, de corresponderende aardrotatietijd en afstand over de aardbol ^[2] op de evenaar.

	Hoek	Uurcirkel	Afstand over de evenaar
Cirkel	360°	24^u	40 075,016 686 kilometer	21 638,777 908 zeemijl
Uur	15°	1^u	1 669,792 362 kilometer	901,615 746 zeemijl
Booggraad	1°	4^m	111,319 491 kilometer	60,107 716 zeemijl
Minuut	15′	1^m	27,829 873 kilometer	15,026 929 zeemijl
Boogminuut	1′	4^s	1 855,325 meter	1,001 795 zeemijl
Kilometer	32,339 4"	2,155 96^s	1000 meter	0,539 957 zeemijl
Seconde	15″	1^s	463,831 meter	0,250 449 zeemijl
Boogseconde	1″	0,066 67^s	30,922 meter	0,016 697 zeemijl

"Hoek" in het dagelijks taalgebruik

Het woord hoek wordt veel gebruikt in de Nederlandse taal:

Hij komt grappig uit de hoek.
Het hoekje om gaan. – eufemisme voor sterven
In de hoek staan. – voor straf in de klas in de hoek worden gezet
Het gezin is de hoeksteen van de samenleving. – metafoor waarin de samenleving voorgesteld wordt als een boog en het gezin als de 'sluitsteen' die het geheel stabiel maakt.
De wind waait uit een andere hoek. – De uitdrukking komt uit de scheepvaart en betekent figuurlijk dat veel zal gaan veranderen.
Het Duitse woord voor hoek is Winkel. Dit komt in het Nederlands terug in het woord winkelhaak. Het Nederlandse woord winkel is afgeleid van de hoeken van (kerk-)gebouwen waarin vaak verkoopkramen stonden.

Voetnoten

↑ R Coolman. Keeping Time: Why 60 Minutes?, 22 september 2022.
↑ GRS 80-referentie-ellipsoïde

[1] R Coolman. Keeping Time: Why 60 Minutes?, 22 september 2022.

[2] GRS 80-referentie-ellipsoïde

[1]

[2]

Anonieme gebruiker

Zoeken

Hoek (meetkunde)

Naamruimten

Meer

Pagina-handelingen

Inhoud